一、概念

（一）引出

TOPSIS优劣解距离法，是一种常用的总和评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距，一般用于评价类问题。

第一讲中提及，层次分析法（第1讲 层次分析法）存在一些局限性，其无法处理太多指标维度的数据，同时其主观性较强，在使用客观数据时，将客观数据转换成得分的标准不固定，因此在解释过程中可能存在一些严谨性问题。

如果直接根据客观数据的大小进行排名，会损失一些信息，如图。

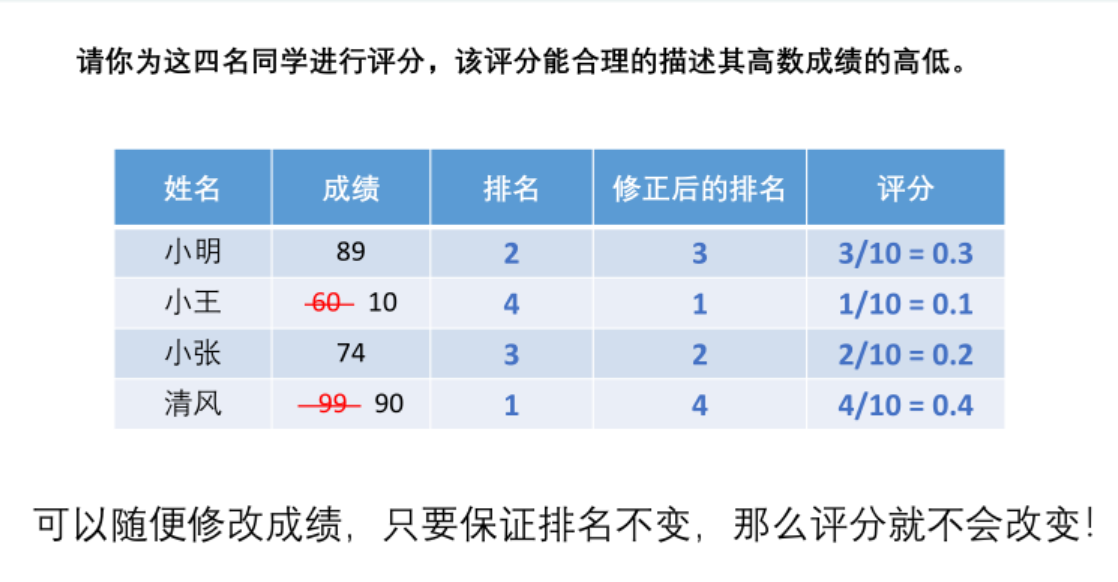
因此这里采用TOPSIS方法进行评价。

（二）问题

TOPSIS方法是在样本内部进行比较，通过对比该相对于所有样本中最优解与最劣解之间的距离，进行比较，从而做出评价。距离最优解越近，最劣解越远的样本越好。

这样就存在一个小问题：为什么不直接算距离可能的最优解与最劣解的距离而要算样本中的最优解与最劣解？
答：
（1）某些指标并没有客观的上限，即没有已知的最优解与最劣解，如国民经济总值。
（2）TOPSIS评价时，评价的对象一般远大于两个，这样，与直接用客观的最优与最劣解相似，当值转变时，除了最优和最劣的值仍然是1与0之外，其他的值均会随着自身的变化而变化，换言之，这两种方法实际的差距在于样本中最优解与最劣解的值始终是1与0，但是因为样本数量较多，因此这两个值不变对整体的影响并不大。
（3）评价过程中存在多个指标，某一个对象在一个指标中可能是最优解/最劣解导致变化不大，但是它在其他指标中可能会变化，因此再次减少了样本中最优解与最劣解值不变的影响。

（三）公式

其中x为样本值，min为样本最劣解，max为样本最优解。

二、步骤

（一）指标正向化（去极性）

需要将所有指标转换为正向指标，即极大型指标（值越大越好）

如何进行指标转换？
最常见的四种指标

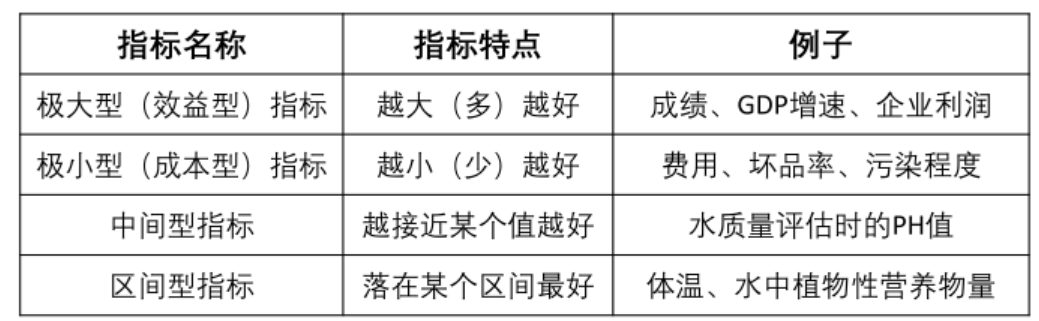
1.极小型——极大型

2.中间型——极大型

3.区间型——极大型

注：公式不唯一，可以根据情况进行适当修改

（二）标准化（去量纲）

标准化的方式有很多种，其主要目的是消去量纲的影响，具体采用什么标准化的方式在大多数情况下并没有限制。
这里采用前人论文中比较多的一种标准化方法。

（三）计算得分并归一化

需要区分标准化与归一化的不同：
归一化的计算步骤也可以消去量纲的影响，但是两者的目标不同，归一化的目的是为了让结果更容易解释，例如将得分归一化到0-1的区间内，对区间中的每一个得分，我们可以很容易得到其所处的比例位置。

三、应用拓展

（一）考虑指标权重

在计算数据与最优解与最劣解的距离时加上权重。
权重如何确定？

1.层次分析法

可以通过层次分析法确定指标权重

2.熵权法

熵权法利用数据本身的特性确定数据的权重。一般来说，数据当中信息量越多的数据应该拥有的权重越高。

如何确定当前指标的信息量？
一件事情发生时信息量的多少往往与其发生的概率相关。一件事情发生的概率越大，当前我们掌握的信息越多，而其真正发生时事件发生蕴含的信息量就越少，信息量与概率之间存在函数关系。

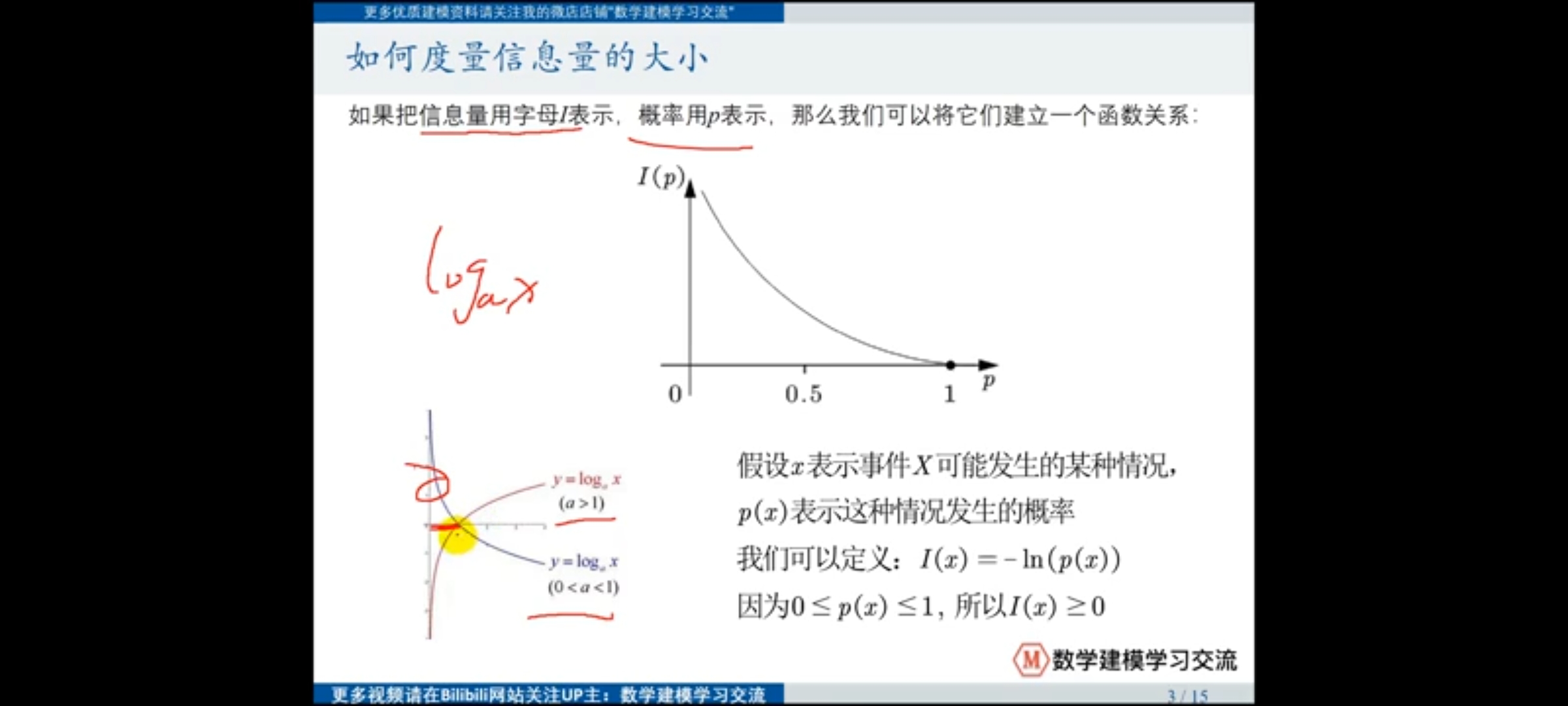
指标信息熵指的是指标中事件发生时信息量的期望值，即事件信息量及其概率的乘积之和，当事件发生的概率相同时，该指标的信息熵最大。

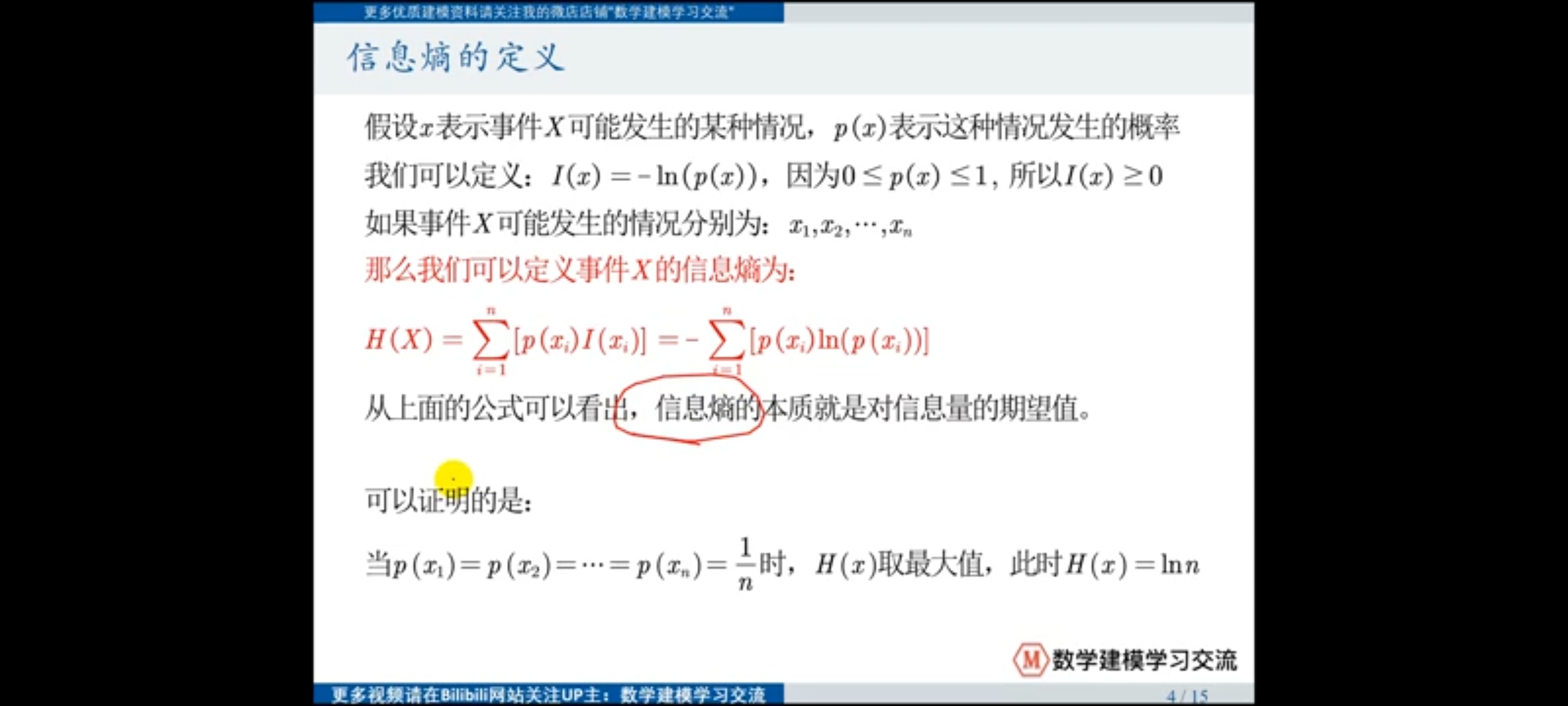
衡量指标的信息量，可以通过指标的信息熵来确定，信息熵指的是指标中事件发生时的期望信息量，当其期望信息量越多，意味着当前指标的信息量越少，通过这种方式可以获得指标的信息量。

计算步骤如下：
（1）非负正向化标准化

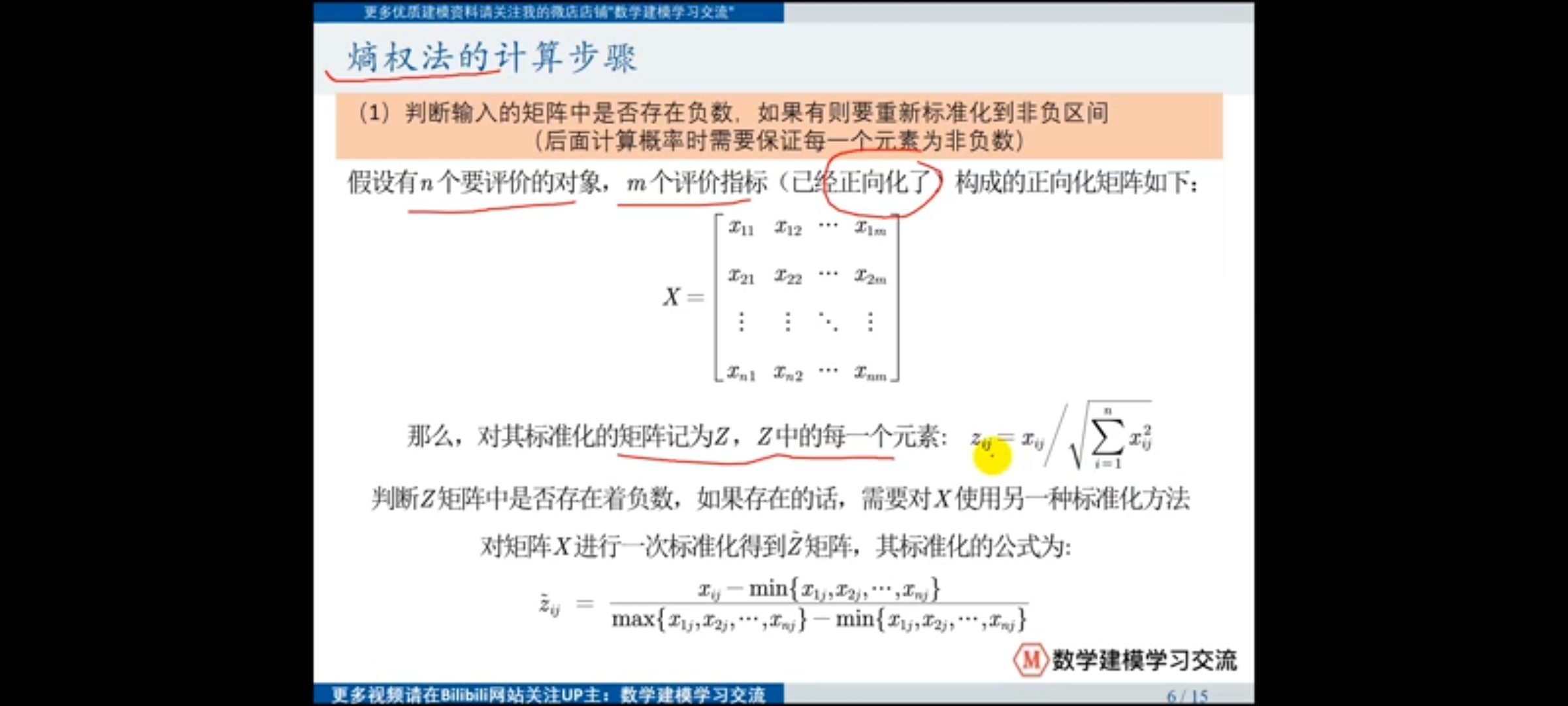
（2）计算比重获得概率

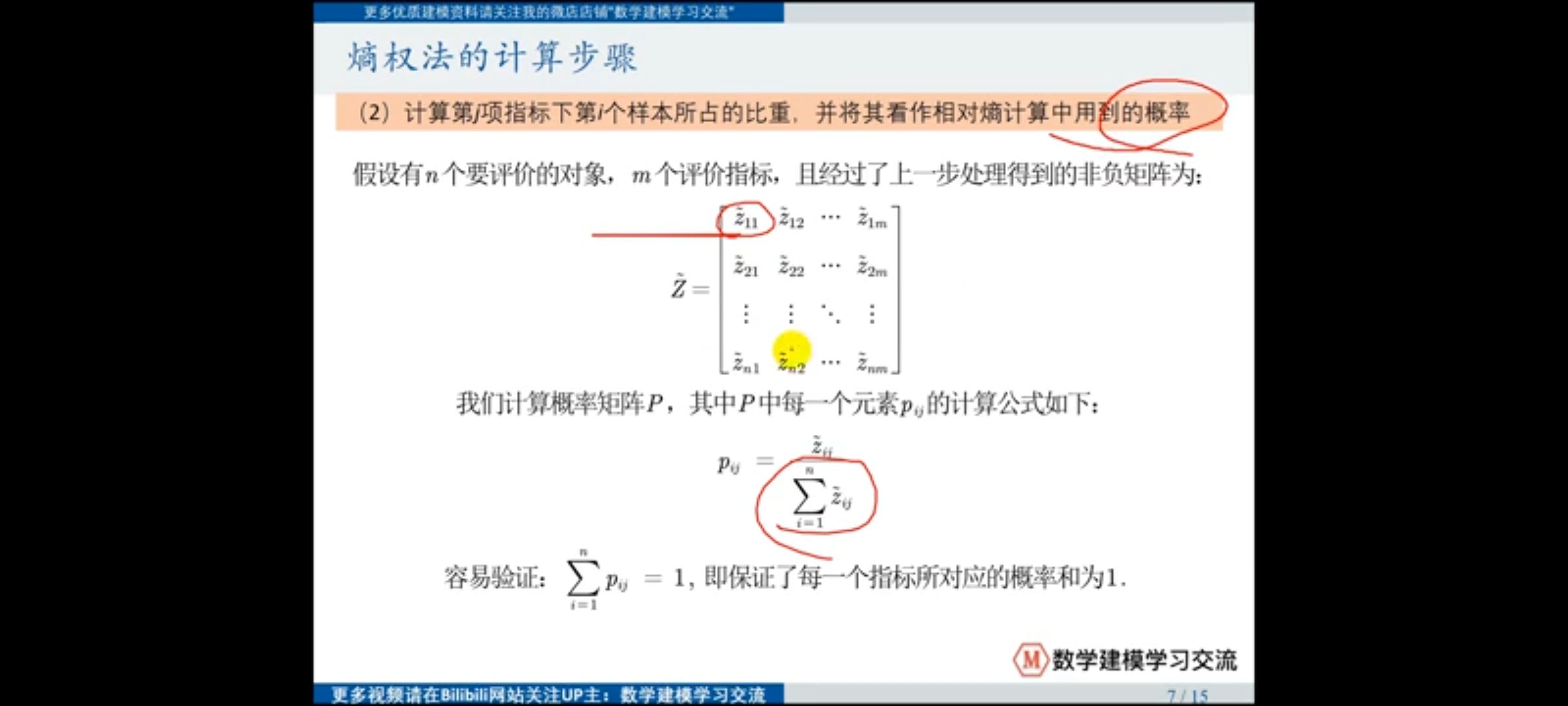
（3）计算信息熵获得信息的效用值

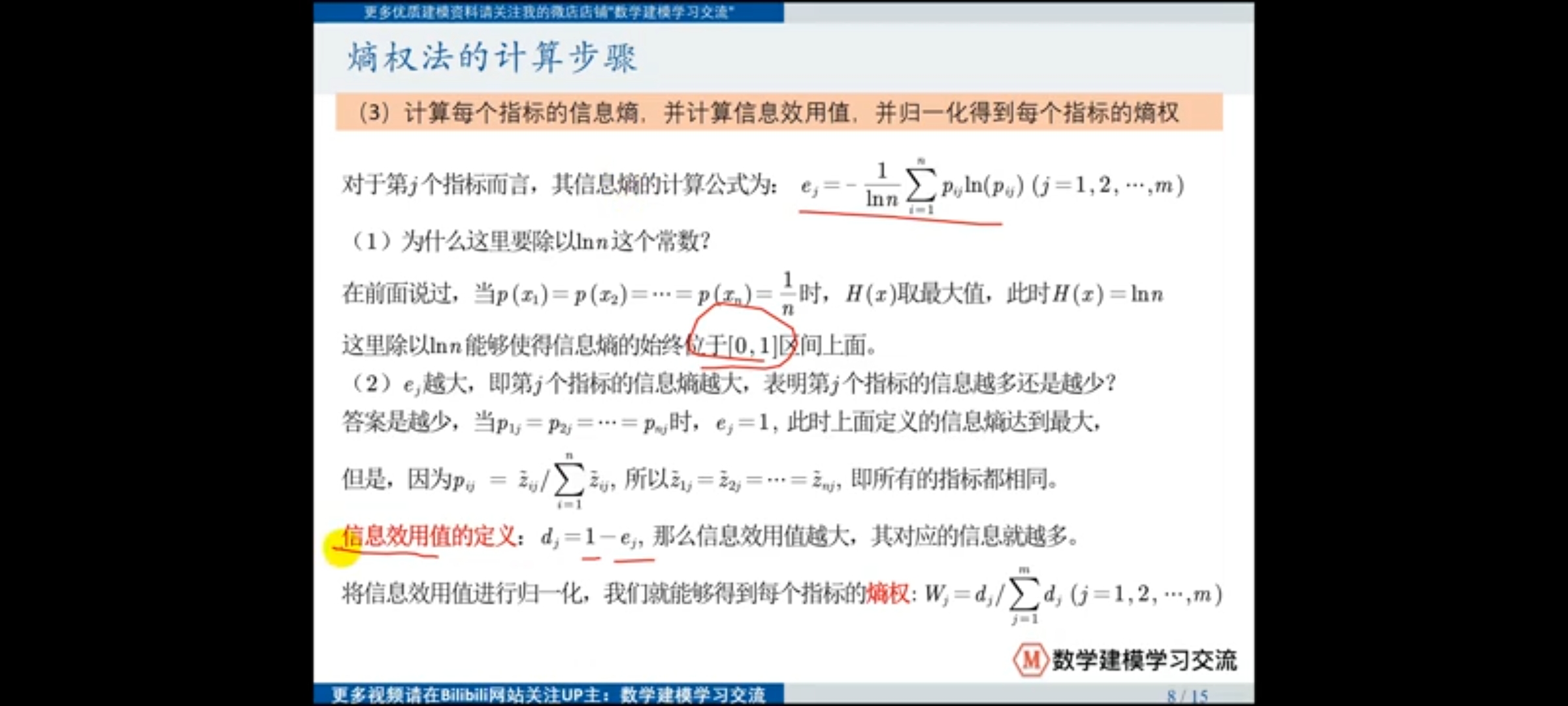
思考：通过比重的方式计算概率这个方法是否可以优化？