一、层次分析法概念

（一）引出

为什么要使用层次分析法？
在处理评价类问题时，如果直接对多个方案进行评价，可能会存在考虑不周或者遗漏信息的情况。层次分析法提供了一个系统的方法帮助进行评价，它将指标两两进行比较，减轻了评价者的认知负荷，便于评价者综合多方面因素，条理清晰地完成对事物的评价。
当我们想要采用层次分析法解决问题时，重点在于完成这个表格。

（二）层级结构

1.目标层

识别决策目标，判断需要解决什么问题，评价目的是什么。

2.准则层

通过什么标准/准则选择方案以实现目标。
一般来说，题目中的目标与方案往往是已知的，重点在于以什么方法进行评价，这里的评价准则需要依据，因此可以根据题目中的背景材料，常识，以及网上搜集到的参考材料进行结合，从其中找到合适的指标
如果没有找到合适的参考文献可以进行头脑风暴或找其他专家的看法

3.方案层

为了实现目标有什么方案

二、什么时候使用层次分析法

评价类问题

层次分析法一般针对评价类问题，而且是客观数据较少的评价类问题，但是实际上，层次分析法的扩展也可以主观数据与客观数据相结合，将客观数据去极性，去量纲之后转换为评分，之后利用层次分析法进行求解，不过相对来说，由于一般层次分析法的主观性较强，因此可能不推荐直接在数学建模中使用。

三、层次分析法步骤

（一）构建层次结构

根据题意，判断是否为评价类问题，找到评价的目标层，准则层，方案层，需要注意的是，准则层可能不止一层，其下可能还有子准则层等，但是无论层次分析法一共分为多少层，其步骤都是找到某一层相对上一层特征的得分，只需要层层进行即可。
需要画出可视化的层次结构图

（二）构建判断矩阵

在层次分析法中，每一层都要获得一个针对上一层指标的得分/权重，那么这个得分/权重从哪里来呢，简单来说就是构建一个判断矩阵。
这个判断矩阵是一个方阵，同时是一个正互反矩阵，主对角线为1，其中aij是指相对于j来说i的重要程度。

（三）获得权重与得分

在构建完判断矩阵之后，通过判断矩阵，我们需要得出某一个特征针对上一层指标的值，如何进行计算呢？

1.矩阵一致性检验

一致矩阵：（各行（各列）成比例）若正互反矩阵（判断矩阵）满足aijxajk=aik，则我们称其为一致矩阵。
在进行计算前，我们首先要进行矩阵一致性检验，保证构建的判断矩阵的内部不存在隐含的矛盾或者其矛盾可接受。

一致检验步骤如下：
（1）求取一致性指标CI

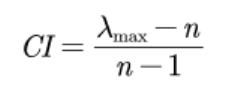
（2）查找对应的平均随机一致性指标RI
（3）计算一致性比例CR=CI/RI，一般CR<0.1，则认为矩阵可以被接受，如果不符合这个条件，则调整判断矩阵

2.标准化（将数据按列归一）

3.求权重

（1） 算数平均法求权重

直接按行相加除以行数

（2）集合平均法求权重

将向量的每个分量开n次方
对该列向量进行归一化即可得到权重向量

（3）特征值法求权重

找到按列归一后的矩阵的最大特征值以及其对应的特征向量
对求出的特征向量进行归一化即可得到权重

在实际的应用过程中，可以考虑综合利用三种方法得到权重，求取均值的方式，保证严谨性

（四）评价

通过权重乘以各方案的得分可以得到各方案的最终得分，将得分进行排序可以找到最优方案。

四、层次分析法局限性

1.主观性
2.维度不宜过多

五、拓展应用

1.准则层与方案层不全对应

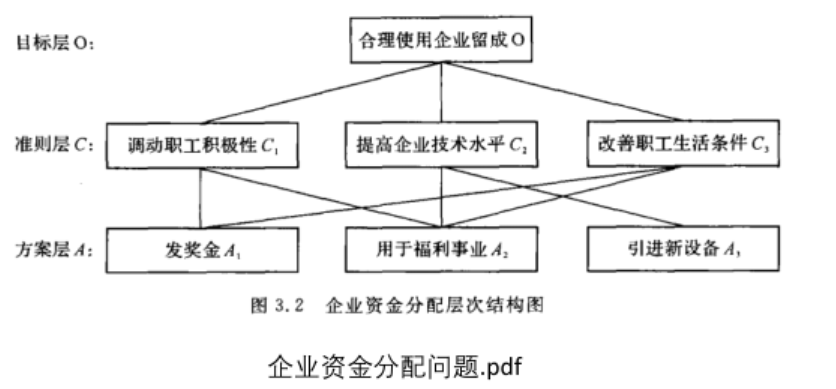
新增线段，将权重设置为0即可

2.准则对应特定方案
直接进行针对指定准则对方案进行评分，之后将准则权重与方案得分相乘排序即可